I recently had a very interesting discussion with my student on topic “Function”. She was not able to appreciate the significance and usage of “Function”.
We tried to connect it to our daily life and after the discussion, she was much comfortable with the topic. We addressed following questions during our discussion.
What is F(x)?
How to Solve G(F(x)) ? What about F(G(x)) ?
What does F mean if I remove x?
What is F(x)?
Me: F(x) is a function which takes input x and gives output F(x).
Student: ??…Ummm…???
Me: Have you ever seen anything like this around you?
Student: Never.
Me: Let’s take a look into your Mum’s kitchen. Have you ever seen a blender there ? She puts tomatoes and blender gives tomato puree.
Student: Yes, I have seen it.
Me: That’s what function is like.

Blender(tomato) = puree
Mathematicians are quite lazy and just manage with initials. So, in a mathematics book, blender function will look something like this.
B(t) = p
This was an example of function from the kitchen.
In mathematics also, Function will look quite similar.

Every function is just like a machine, which takes input and gives us output. Like – Blender, Juicer, Printer, Scanner.
Lets try to understand one simple function. F(x) = 7x + 9
F(x) = 7x + 9

F(3x) = 7*(3x) + 9 = 21x +9

F(4) = 7*4 + 9 = 28 + 9 = 37

F(x+3) = 7* (x+3) + 9 = 7x + 21 + 9 = 7x + 30

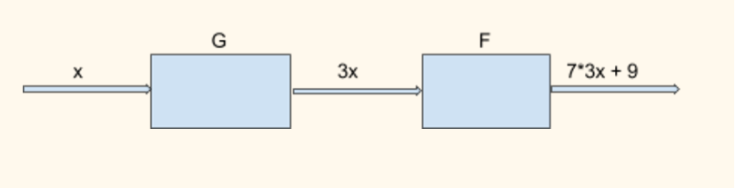
What does G(F(x)) mean ?
Let’s get back to kitchen once again. Let’s say, your mum has one more machine in her kitchen named Roaster. As the name says, roaster roasts the input.
Let’s say R stands for Roaster so how about B(R(t)
B(R(t)) = Blender(Roaster(tomato))
= Blender(roasted tomato)
= Roasted tomato puree

If you are clear with this explanation, I am sure you must have got visual understanding of mathematical functions as well.
If , F(x) = 7x + 9
G(x) = 3x
Then , G(F(x)) = G(7x +9) = 3 * ( 7x +9 ) = 21x +27

F(G(x)) = F(3x) =7*3x + 9 = 21x +9
What does F mean if I remove x?
Let’s look back at the example of Blender.
Blender(tomato) = puree
Blender only works when we provide tomato as ‘input’.
That’s the same way in Mathematics as well.
Function will only work when provided with ‘input’
“F without x” is exactly same as “Blender without tomato”.
Proper introduction of the concept plays a key role in further learning. Introduction should be as intuitive as possible and it should be very close to our students’ lives so that they can grasp the concept just like 1, 2, 3.
